Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Compute and visualise kinematics.#
Compute displacement, velocity and acceleration, and visualise the results.
Imports#
# For interactive plots: install ipympl with `pip install ipympl` and uncomment
# the following line in your notebook
# %matplotlib widget
from matplotlib import pyplot as plt
import movement.kinematics as kin
from movement import sample_data
from movement.plots import plot_centroid_trajectory
from movement.utils.vector import compute_norm
Load sample dataset#
First, we load an example dataset. In this case, we select the
SLEAP_three-mice_Aeon_proofread sample data.
ds = sample_data.fetch_dataset(
"SLEAP_three-mice_Aeon_proofread.analysis.h5",
)
print(ds)
<xarray.Dataset> Size: 27kB
Dimensions: (time: 601, space: 2, keypoints: 1, individuals: 3)
Coordinates:
* time (time) float64 5kB 0.0 0.02 0.04 0.06 ... 11.96 11.98 12.0
* space (space) <U1 8B 'x' 'y'
* keypoints (keypoints) <U8 32B 'centroid'
* individuals (individuals) <U10 120B 'AEON3B_NTP' 'AEON3B_TP1' 'AEON3B_TP2'
Data variables:
position (time, space, keypoints, individuals) float32 14kB 770.3 ......
confidence (time, keypoints, individuals) float32 7kB nan nan ... nan nan
Attributes:
source_software: SLEAP
ds_type: poses
fps: 50.0
time_unit: seconds
source_file: /home/runner/.movement/data/poses/SLEAP_three-mice_Aeon...
frame_path: /home/runner/.movement/data/frames/three-mice_Aeon_fram...
We can see in the printed description of the dataset ds that
the data was acquired at 50 fps, and the time axis is expressed in seconds.
It includes data for three individuals(AEON3B_NTP, AEON3B_TP1,
and AEON3B_TP2), and only one keypoint called centroid was tracked
in x and y dimensions.
The loaded dataset ds contains two data arrays:
position and confidence.
To compute displacement, velocity and acceleration, we will need the
position one:
Visualise the data#
First, let’s visualise the trajectories of the mice in the XY plane,
colouring them by individual.
We use movement.plots.plot_centroid_trajectory() which is a wrapper
around matplotlib.pyplot.scatter() that simplifies plotting the
trajectories of individuals in the dataset.
The fig and ax objects returned can be used to further customise the plot.
# Create a single figure and axes
fig, ax = plt.subplots(1, 1)
# Invert y-axis so (0,0) is in the top-left,
# matching typical image coordinate systems
ax.invert_yaxis()
# Plot trajectories for each mouse on the same axes
for mouse_name, col in zip(
position.individuals.values,
["r", "g", "b"], # colours
strict=False,
):
plot_centroid_trajectory(
position,
individual=mouse_name,
ax=ax, # Use the same axes for all plots
c=col,
marker="o",
s=10,
alpha=0.2,
label=mouse_name,
)
ax.legend().set_alpha(1)
fig.show()
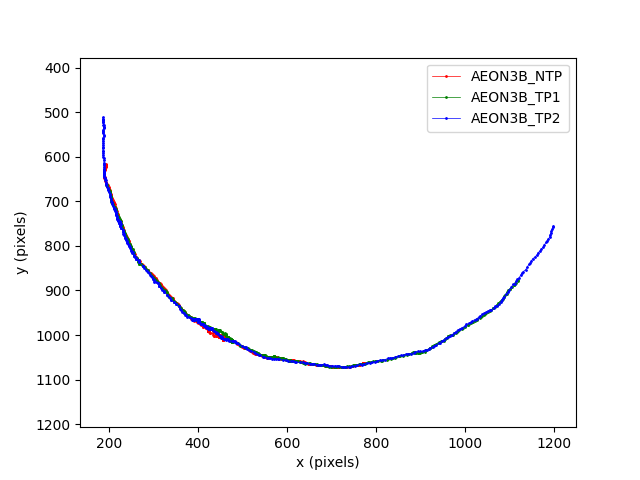
We can see that the trajectories of the three mice are close to a circular arc. Notice that the x and y axes are set to equal scales, and that the origin of the coordinate system is at the top left of the image. This follows the convention for SLEAP and most image processing tools.
By default plot_centroid_trajectory() colours data points based on their timestamps:
fig, axes = plt.subplots(3, 1, sharey=True)
for mouse_name, ax in zip(position.individuals.values, axes, strict=False):
ax.invert_yaxis()
fig, ax = plot_centroid_trajectory(
position,
individual=mouse_name,
ax=ax,
s=2,
)
ax.set_title(f"Trajectory {mouse_name}")
ax.set_xlabel("x (pixels)")
ax.set_ylabel("y (pixels)")
ax.collections[0].colorbar.set_label("Time (frames)")
fig.tight_layout()
fig.show()
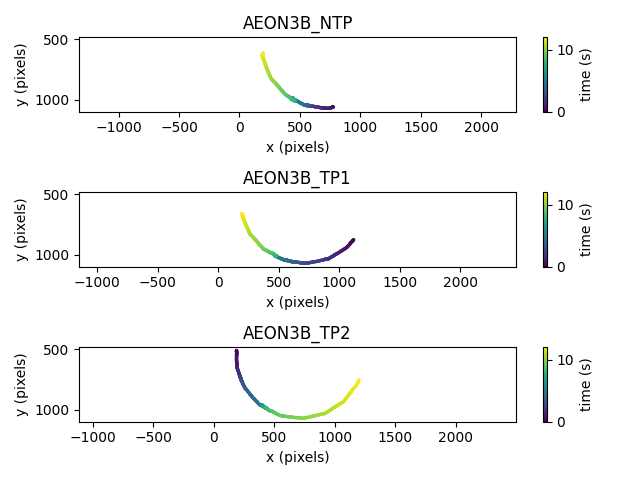
These plots show that for this snippet of the data,
two of the mice (AEON3B_NTP and AEON3B_TP1)
moved around the circle in clockwise direction, and
the third mouse (AEON3B_TP2) followed an anti-clockwise direction.
We can also easily plot the components of the position vector against time
using xarray’s built-in plotting methods. We use
xarray.DataArray.squeeze() to
remove the dimension of length 1 from the data (the keypoints dimension).
position.squeeze().plot.line(x="time", row="individuals", aspect=2, size=2.5)
plt.gcf().show()
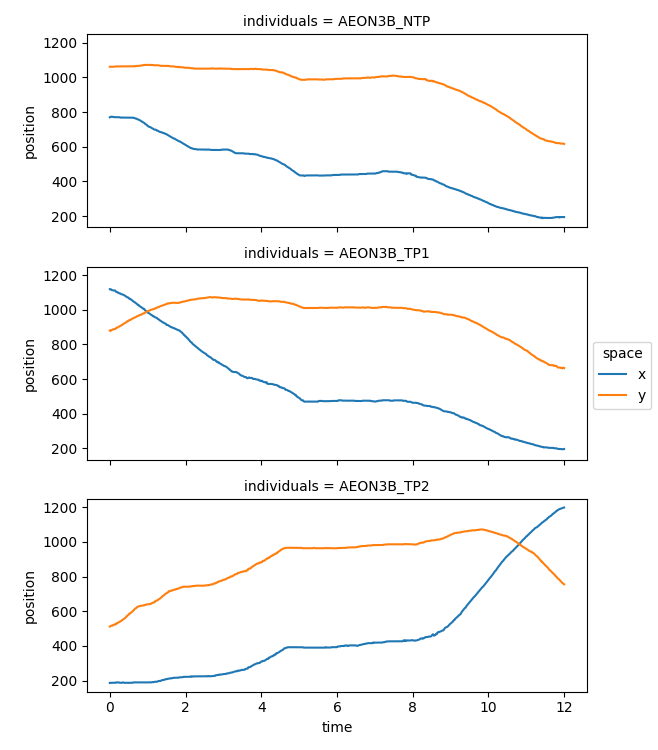
If we use xarray’s plotting function, the axes units are automatically
taken from the data array. In our case, time is expressed in seconds,
and the x and y coordinates of the position are in pixels.
Compute displacement#
The movement.kinematics module
provides functions to compute various kinematic quantities,
such as displacement, velocity, and acceleration.
We can start off by computing the distance travelled by the mice along
their trajectories:
The movement.kinematics.compute_displacement()
function will return a data array equivalent to the position one,
but holding displacement data along the space axis, rather than
position data.
The displacement data array holds, for a given individual and keypoint
at timestep t, the vector that goes from its previous position at time
t-1 to its current position at time t.
And what happens at t=0, since there is no previous timestep?
We define the displacement vector at time t=0 to be the zero vector.
This way the shape of the displacement data array is the
same as the position array:
print(f"Shape of position: {position.shape}")
print(f"Shape of displacement: {displacement.shape}")
Shape of position: (601, 2, 1, 3)
Shape of displacement: (601, 2, 1, 3)
We can visualise these displacement vectors with a quiver plot. In this case
we focus on the mouse AEON3B_TP2:
mouse_name = "AEON3B_TP2"
fig = plt.figure()
ax = fig.add_subplot()
# plot position data
sc = ax.scatter(
position.sel(individuals=mouse_name, space="x"),
position.sel(individuals=mouse_name, space="y"),
s=15,
c=position.time,
cmap="viridis",
)
# plot displacement vectors: at t, vector from t-1 to t
ax.quiver(
position.sel(individuals=mouse_name, space="x"),
position.sel(individuals=mouse_name, space="y"),
displacement.sel(individuals=mouse_name, space="x"),
displacement.sel(individuals=mouse_name, space="y"),
angles="xy",
scale=1,
scale_units="xy",
headwidth=7,
headlength=9,
headaxislength=9,
)
ax.axis("equal")
ax.set_xlim(450, 575)
ax.set_ylim(950, 1075)
ax.set_xlabel("x (pixels)")
ax.set_ylabel("y (pixels)")
ax.set_title(f"Zoomed in trajectory of {mouse_name}")
ax.invert_yaxis()
fig.colorbar(sc, ax=ax, label="time (s)")
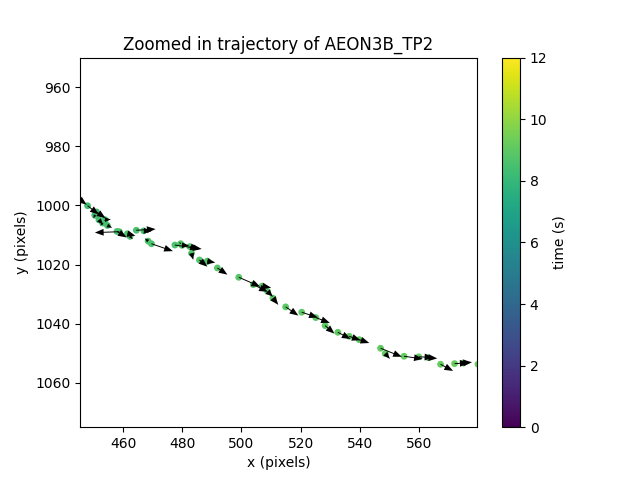
<matplotlib.colorbar.Colorbar object at 0x7fc0ba69b650>
Notice that this figure is not very useful as a visual check:
we can see that there are vectors defined for each point in
the trajectory, but we have no easy way to verify they are indeed
the displacement vectors from t-1 to t.
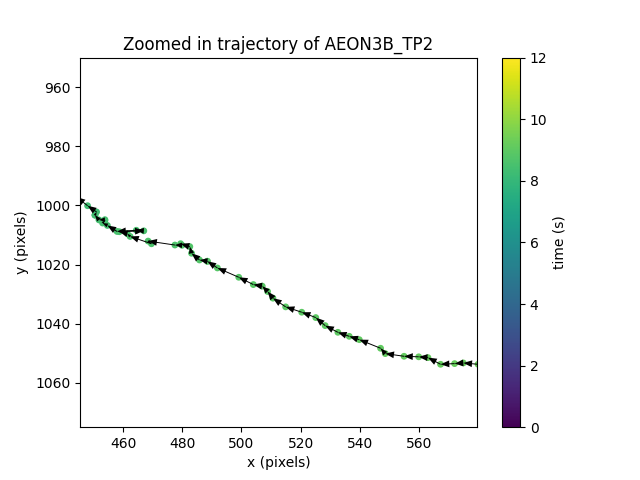
If instead we plot
the opposite of the displacement vector, we will see that at every time
t, the vectors point to the position at t-1.
Remember that the displacement vector is defined as the vector at
time t, that goes from the previous position t-1 to the
current position at t. Therefore, the opposite vector will point
from the position point at t, to the position point at t-1.
We can easily do this by flipping the sign of the displacement vector in the plot above:
mouse_name = "AEON3B_TP2"
fig = plt.figure()
ax = fig.add_subplot()
# plot position data
sc = ax.scatter(
position.sel(individuals=mouse_name, space="x"),
position.sel(individuals=mouse_name, space="y"),
s=15,
c=position.time,
cmap="viridis",
)
# plot displacement vectors: at t, vector from t-1 to t
ax.quiver(
position.sel(individuals=mouse_name, space="x"),
position.sel(individuals=mouse_name, space="y"),
-displacement.sel(individuals=mouse_name, space="x"), # flipped sign
-displacement.sel(individuals=mouse_name, space="y"), # flipped sign
angles="xy",
scale=1,
scale_units="xy",
headwidth=7,
headlength=9,
headaxislength=9,
)
ax.axis("equal")
ax.set_xlim(450, 575)
ax.set_ylim(950, 1075)
ax.set_xlabel("x (pixels)")
ax.set_ylabel("y (pixels)")
ax.set_title(f"Zoomed in trajectory of {mouse_name}")
ax.invert_yaxis()
fig.colorbar(sc, ax=ax, label="time (s)")
<matplotlib.colorbar.Colorbar object at 0x7fc0c95d56d0>
Now we can visually verify that indeed the displacement vector connects the previous and current positions as expected.
With the displacement data we can compute the distance travelled by the mouse along its trajectory.
# length of each displacement vector
displacement_vectors_lengths = compute_norm(
displacement.sel(individuals=mouse_name)
)
# sum the lengths of all displacement vectors (in pixels)
total_displacement = displacement_vectors_lengths.sum(dim="time").values[0]
print(
f"The mouse {mouse_name}'s trajectory is {total_displacement:.2f} "
"pixels long"
)
The mouse AEON3B_TP2's trajectory is 1640.09 pixels long
Compute velocity#
We can easily compute the velocity vectors for all individuals in our data array:
The movement.kinematics.compute_velocity()
function will return a data array equivalent to
the position one, but holding velocity data along the space axis,
rather than position data. Notice how xarray nicely deals with the
different individuals and spatial dimensions for us! ✨
We can plot the components of the velocity vector against time
using xarray’s built-in plotting methods. We use
xarray.DataArray.squeeze() to
remove the dimension of length 1 from the data (the keypoints dimension).
velocity.squeeze().plot.line(x="time", row="individuals", aspect=2, size=2.5)
plt.gcf().show()
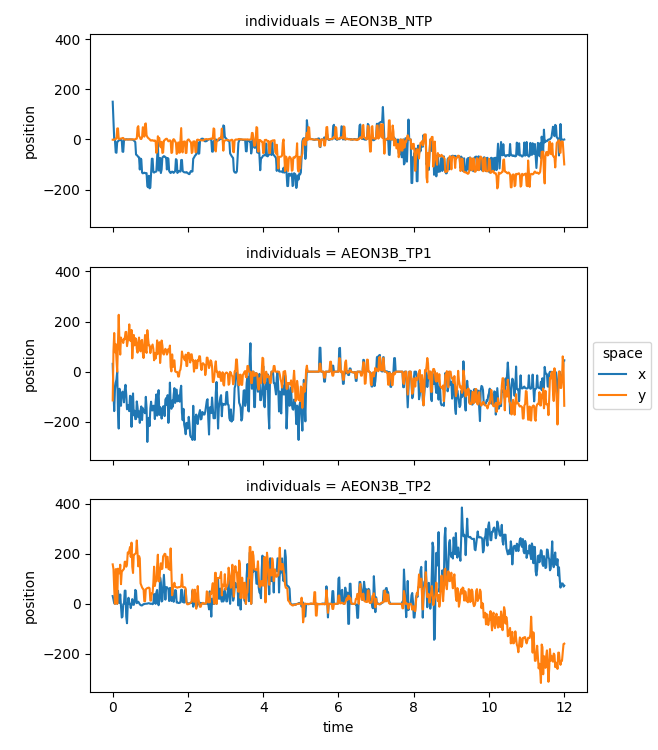
The components of the velocity vector seem noisier than the components of the position vector. This is expected, since we are deriving the velocity using differences in position (which is somewhat noisy), over small stepsizes. More specifically, we use numpy’s gradient implementation, which uses second order central differences.
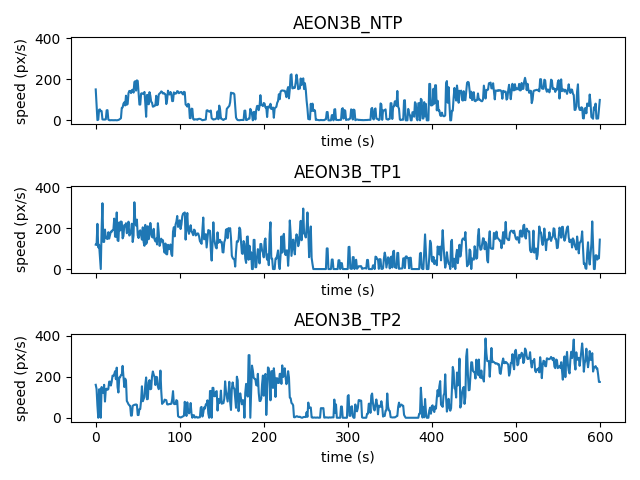
We can also visualise the speed, as the magnitude (norm) of the velocity vector:
fig, axes = plt.subplots(3, 1, sharex=True, sharey=True)
for mouse_name, ax in zip(velocity.individuals.values, axes, strict=False):
# compute the magnitude of the velocity vector for one mouse
speed_one_mouse = compute_norm(velocity.sel(individuals=mouse_name))
# plot speed against time
ax.plot(speed_one_mouse)
ax.set_title(mouse_name)
ax.set_xlabel("time (s)")
ax.set_ylabel("speed (px/s)")
fig.tight_layout()
To visualise the direction of the velocity vector at each timestep, we can use a quiver plot:
mouse_name = "AEON3B_TP2"
fig = plt.figure()
ax = fig.add_subplot()
# plot trajectory (position data)
sc = ax.scatter(
position.sel(individuals=mouse_name, space="x"),
position.sel(individuals=mouse_name, space="y"),
s=15,
c=position.time,
cmap="viridis",
)
# plot velocity vectors
ax.quiver(
position.sel(individuals=mouse_name, space="x"),
position.sel(individuals=mouse_name, space="y"),
velocity.sel(individuals=mouse_name, space="x"),
velocity.sel(individuals=mouse_name, space="y"),
angles="xy",
scale=2,
scale_units="xy",
color="r",
)
ax.axis("equal")
ax.set_xlabel("x (pixels)")
ax.set_ylabel("y (pixels)")
ax.set_title(f"Velocity quiver plot for {mouse_name}")
ax.invert_yaxis()
fig.colorbar(sc, ax=ax, label="time (s)")
fig.show()
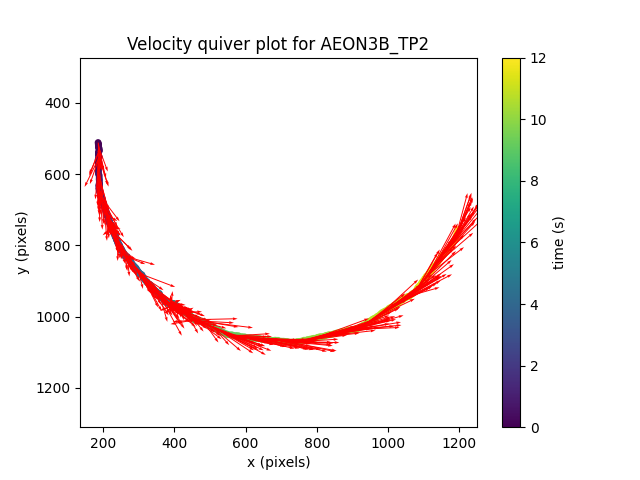
Here we scaled the length of vectors to half of their actual value
(scale=2) for easier visualisation.
Compute acceleration#
Let’s now compute the acceleration for all individuals in our data array:
and plot of the components of the acceleration vector ax, ay per
individual:
fig, axes = plt.subplots(3, 1, sharex=True, sharey=True)
for mouse_name, ax in zip(accel.individuals.values, axes, strict=False):
# plot x-component of acceleration vector
ax.plot(
accel.sel(individuals=mouse_name, space=["x"]).squeeze(),
label="ax",
)
# plot y-component of acceleration vector
ax.plot(
accel.sel(individuals=mouse_name, space=["y"]).squeeze(),
label="ay",
)
ax.set_title(mouse_name)
ax.set_xlabel("time (s)")
ax.set_ylabel("speed (px/s**2)")
ax.legend(loc="center right", bbox_to_anchor=(1.07, 1.07))
fig.tight_layout()
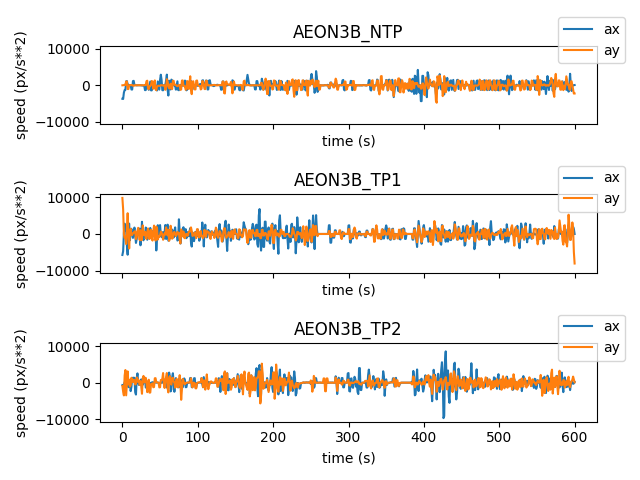
We can also compute and visualise the magnitude (norm) of the acceleration vector for each individual:
fig, axes = plt.subplots(3, 1, sharex=True, sharey=True)
for mouse_name, ax in zip(accel.individuals.values, axes, strict=False):
# compute magnitude of the acceleration vector for one mouse
accel_one_mouse = compute_norm(accel.sel(individuals=mouse_name))
# plot acceleration against time
ax.plot(accel_one_mouse)
ax.set_title(mouse_name)
ax.set_xlabel("time (s)")
ax.set_ylabel("accel (px/s**2)")
fig.tight_layout()
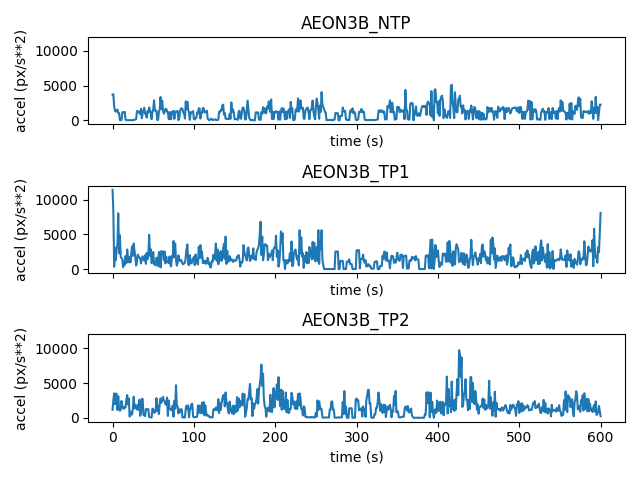
Total running time of the script: (0 minutes 1.987 seconds)